Übung 2, Abgabe bis 21.12.2016 24:00
4. Bayes'sche Entscheidungstheorie und Anwendungen (5 Pkt)
Eine weit verbreitete Art einen Klassifikator darzustellen ist mit Hilfe von Diskriminantenfunktionen gi(x).Der Klassifikator weist einem Merkmalsvektor x die Klasse ωi zu, wenn gi(x) > gj(x) für alle j <> i.
Betrachten Sie zwei normalverteilte Klassen:
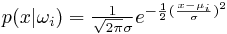 (Formel für Normalverteilung)
(Formel für Normalverteilung)mit Standardabweichung σ = 1 und A Priori-Wahrscheinlickeiten P(ω1) = P(ω2).
Berechnen Sie einen Klassifikator mit minimalem (bayes'schem) Fehler folgendermaßen: Leiten Sie aus obiger Gleichung die A-Posteriori Wahrscheinlichkeit P(ωi|x) ab. Definieren Sie anschließend die logarithmische Diskriminantenfunktion gi(x) = log P(ωi | x).
Verwenden Sie die logarithmischen Form der Diskriminatenfunktion um in allgemeiner Form die Entscheidungsgrenze zu berechnen, d.h. den Wert von x für den g1(x) = g2(x) ist.
Verifizieren Sie Ihr Ergebnis für μ1 = 2 und μ2 = 4. Geben Sie Klassifikationsregeln in Form von Wenn-Dann Regeln an.
5. Anwendungen der Bayes'schen Entscheidungstheorie (4+4+6 Pkt)
-
Dr. X ist Mediziner und an Statistik interessiert. Er verwendet einen bestimmten Test um zu bestimmen, ob sein Patient Y an Krebs erkrankt ist. Leider ist der Test nicht 100% zuverlässig. Genaugenommen zeigt der Test nur in 98% aller Krebsfälle diese auch an. Im Fall dass der Patient nicht Krebs hat, besteht immer noch eine 3%-ige Wahrscheinlichkeit, dass der Test dennoch positiv ausfällt. Im Schnitt haben 0,8% der Gesamtbevölkerung Krebs.
Wie hoch ist die Wahrscheinlichkeit, dass Patient Y Krebs hat, wenn der Test positiv ist? Nach dem positiven Ergebnis, beschließt der Arzt, den Test zu wiederholen. Der zweite Test ist ebenfalls positiv. Wie hoch ist die Wahrscheinlichkeit nun? (Unter der Annahme, dass die Tests statistisch unabhängig sind.) - Sie installieren Ihr neues Bildverarbeitungssystem in einer Chipfabrik, das 95% aller kaputten Chips entdeckt, allerdings auch bei 1% der funktionsfähigen Chips Alarm schlägt. Insgesamt sind 1% aller Chips Ausschuß. Die Herstellungskosten für einen Chip betragen 5 EUR, der Verkaufpreis 20 EUR. Die Folgekosten für einen irrtümlich durchgelassenen kaputten Chip sind sehr hoch, nämlich 1995 EUR. Ihr Chef will von Ihnen das erwartete Gesamtrisiko bei Anwendung der optimalen Bayes-Entscheidungsregel wissen, d.h. wieviel Gewinn oder Verlust er in diesem Fall pro Chip machen wird.
-
Eine Fabrik in der normalerweise Apfelsaft produziert wird, wird in
Kriegsjahren dazu verwendet, auch Handgranaten herzustellen. Äpfel
und Granaten werden auch demselben Förderband bewegt. An einer
Stelle werden Äpfel von Granaten aufgrund ihres Gewichts getrennt,
erstere zu Saft verarbeitet, letztere sorgfältig verpackt und
verschickt.
Im Schnitt wiegt ein Apfel 100g mit einer Standardabweichung von 30g und eine Handgranate 250g mit einer Standardabweichung von 5g. Insgesamt sind 80% aller Gegenstände auf dem Förderband Äpfel.
Berechnen Sie eine Klassifikationsregel für Gegenstände auf dem Förderband um die Wahrscheinlichkeit eines Klassifikationsfehlers zu minimieren.
Es ist einsichtig, dass die Fehlklassifikation einer Handgranate als Apfel höchst gefährlich ist. Folglich definieren wir das Risiko (Kosten) einer Klassifikation: Fehlklassifikation einer Granate als Apfel ist 100, Fehlklassifikation eines Apfels als Granate ist 1. Die korrekte Klassifikation hat keine (0) Kosten.
Berechnen Sie eine Klassifikationsregel, welche das Gesamtrisiko minimiert. Wie unterscheidet sich diese Klassifikationsregel von der vorherigen, fehlerminimierenden?
6. Naive Bayes (5 Pkt)
Folgende Trainingsdaten liegen für gestohlene Autos vor:| Example ID | Color | Type | Origin | Stolen? |
|---|---|---|---|---|
| 1 | Red | Sports | Domestic | Yes |
| 2 | Red | Sports | Domestic | No |
| 3 | Red | Sports | Domestic | Yes |
| 4 | Yellow | Sports | Domestic | No |
| 5 | Yellow | Sports | Imported | Yes |
| 6 | Yellow | SUV | Imported | No |
| 7 | Yellow | SUV | Imported | Yes |
| 8 | Yellow | SUV | Domestic | No |
| 9 | Red | SUV | Imported | No |
| 10 | Red | Sports | Imported | Yes |
7. Wahrscheinlichkeitsdichteschätzung (6 Pkt)
Die Datei samples.rda enthält ingesamt 70 Beobachtungen für 2 unterschiedliche Klassen. Laden Sie die Daten nach R oder in ein anderes Tool ihrer Wahl (load('samples.rda') lädt die Daten in die Variable d) und berechnen Sie die Likelihood für die beiden Testpunkte (6/4) und (4/0) auf folgende beide Arten.- Parametrisch: Maximum Likelihood Estimate
Gehen Sie davon aus, dass beide Klassen von einer bivariaten Normalverteilung generiert wurden. Schätzen Sie mittels der R Funktion mlest aus dem Package mvnmle Mittelwert und Kovarianz für jede der beiden Klassen. Berechnen Sie anschließend die Likelihood (siehe Funktion dmvnorm) für jeden der beiden gefragten Punkte und jede der beiden Klassen. - Nichtparametrisch: Parzen-Window
Diesmal haben Sie keine Information über die klassenbedingte Verteilung, deshalb wählen Sie einen nichtparametrischen Ansatz. Verwenden Sie die Funktion bkde2D aus dem package KernSmooth zur Dichteschätzung. bkde2D benötigt die Angabe eines Bandbreitevektors c(bx,by). Probieren Sie verschiedene Bandbreiten und beurteilen Sie diese anhand des Contourplots der geschätzen Dichtefunktion. (Hinweis: est <- bkde2D(....); contour(est$x1,est$x2, est$fhat) ).
Wählen Sie eine konkrete Schätzung und bestimmen Sie wie für Aufgabe a) die Likelihood für beide Punkte und jede der beiden Klassen. (Hinweis: Finden Sie die korrekte Zelle in est$fhat indem Sie zuerst die richtige Zeile und Spalte in est$x1 bzw. est$x2 finden.) - Klassifikation
Wie würden die beiden Punkte in jedem der beiden Ansätze klassifiziert? Basiert Ihre Antwort auf Maximum Likelihood (ML) oder Maximum Posteriori (MAP)? Wie sieht jeweils die andere Möglichkeit aus?
